Hàm số liên tục là gì? Phương pháp giải và Các dạng bài tập
Chức năng liên tục Nó là một phần lý thuyết quan trọng trong chương trình học toán của học sinh. Vì vậy, định nghĩa. Trong phạm vi bài viết dưới đây, Tip.edu.vn sẽ giúp bạn giải đáp thắc mắc trên, cùng tìm hiểu nhé.
HSLT. học thuyết
Chức năng liên tục tại một điểm
Giả sử cho một hàm (y = f (x) ) được xác định trên ((a; b) ) và (x_ {0} epsilon (a; b) )
Khi đó, hàm (y = f (x) ) liên tục tại (x_ {0} ) ⇔limx → x0f (x) = f (x0) x0⇔limx → x0f (x) = f (x0) )
Để xem xét tính liên tục của hàm (y = f (x) ) Tại điểm (x_ {0} ) Chúng tôi thực hiện các bước sau:
- Bước 1: Tính toán (f (x_ {0}) )
- Bước 2: Tính ( lim_ {x rightarrow x_ {0}} f (x) ) (Trong nhiều trường hợp, chúng ta cần tính ( lim_ {x rightarrow x_ {0 ^ {+}}} f ( x), lim_ {x rightarrow x_ {0 ^ {-}}} f (x) )).
- Bước 3: So sánh ( lim_ {x rightarrow x_ {0}} f (x) ) với (f (x_ {0}) ).
- Bước 4: Kết luận
- Hàm (y = f (x) ) không liên tục tại (x_ {0} ) được cho là không liên tục tại thời điểm đó.
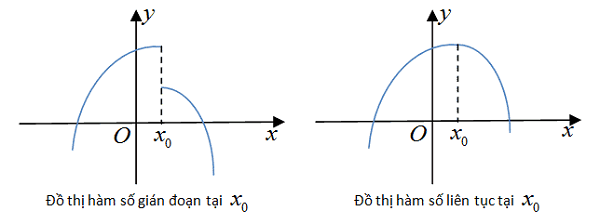
Hàm liên tục trong một khoảng thời gian
Hàm (y = f (x) ) liên tục trên một khoảng nếu nó liên tục tại mọi điểm trong khoảng đó.
Đồ thị của HSLT trên một khoảng là “đường liền nét” trên khoảng đó.
Chức năng liên tục trên phân đoạn
Hàm (y = f (x) ) liên tục trên đoạn ([a;b]) nếu nó liên tục trong khoảng ((a; b) ) và
( lim_ {x rightarrow a ^ {+}} f (x) = f (a), lim_ {x rightarrow b ^ {-}} f (x) = f (b) )
Hàm liên tục trên ( mathbb {R} )
- Đa thức liên tục trên toàn bộ tập số thực ( mathbb {R} ).
- Một hàm phân số hữu tỉ (thương của hai đa thức), một hàm lượng giác liên tục trên mỗi khoảng của tập xác định của chúng.
Giả sử (y = f (x) ) và (y = g (x) ) là hai HSLT tại điểm (x_ {0} ). Sau đó:
- Các hàm (y = f (x) + g (x), y = f (x) -g (x), y = f (x) .g (x) ) liên tục tại (x_ {0) } ).
- Hàm (y = frac {f (x)} {g (x)} ) liên tục tại (x_ {0} ) if (g (x_ {0}) neq 0 ).
Các thuộc tính của hàm liên tục
Định lý
Hàm (y = f (x) ) liên tục trên ([a;b]) và (f (a) neq f (b) Rightarrow forall M ) giữa (f (a), f (b), tồn tại c epsilon (a; b): f (c) = M )
Hệ quả
Hàm (y = f (x) ) liên tục trên ([a;b]) và (f (a) .f (b) <0 Rightarrow tồn tại c epsilon (a; b): f (c) = 0 )
Hệ quả này thường được sử dụng để chứng minh sự tồn tại của một nghiệm của một phương trình trên một khoảng.
Các dạng toán và cách giải
Dạng 1: HSLT tại một điểm
- (f (x) = left { begin {matrix} h (x, m) & (x neq x_ {0}) \ g (x, m) & (x = x_ {0}) end {matrix} right. ) tại (x = x_ {0} )
Phương pháp giải quyết:
Bước 1: Tính toán (f (x_ {0}) )
Bước 2: Tính ( lim_ {x rightarrow x_ {0}} f (x) )
Bước 3: So sánh ( lim_ {x rightarrow x_ {0}} f (x) ) với (f (x_ {0}) )
Bước 4: Kết luận
- (f (x) = left { begin {matrix} h (x, m) & (x geq x_ {0}) \ g (x, m) & (x
hoặc: (f (x) = left { begin {matrix} h (x, m) & (x> x_ {0}) \ g (x, m) & (x leq x_ {0} ) end {matrix} right ) tại (x = x_ {0} )
Phương pháp giải quyết:
Bước 1: Tính toán (f (x_ {0}) )
Bước 2: Tính ( lim_ {x rightarrow x_ {0 ^ {+}}} f (x), lim_ {x rightarrow x_ {0 ^ {-}}} f (x) )
Bước 3: So sánh ( lim_ {x rightarrow x_ {0 ^ {+}}} f (x), lim_ {x rightarrow x_ {0 ^ {-}}} f (x), f (x_ { 0}) )
Bước 4: Kết luận
Loại 2: HSLT trên tập xác định của nó
- (f (x) = left { begin {matrix} h (x, m) & (x neq x_ {0}) \ g (x, m) & (x = x_ {0}) end {matrix} right. )
Phương pháp giải quyết:
Bước 1: Tìm tập xác định của hàm số đã cho
Bước 2: Khi (x neq x_ {0} ), xác định tính liên tục của hàm (f (x) ) tại (x neq x_ {0} )
Bước 3: Khi nào (x = x_ {0} )
- Tính (f (x_ {0}) )
- Tính ( lim_ {x rightarrow x_ {0}} f (x) )
- So sánh ( lim_ {x rightarrow x_ {0}} f (x) ) với (f (x_ {0}) ) và rút ra kết luận tại (x_ {0} )
Bước 4: Kết luận tính liên tục trên tập xác định của chúng.
- (f (x) = left { begin {matrix} h (x, m) & (x geq x_ {0}) \ g (x, m) & (x
hoặc: (f (x) = left { begin {matrix} h (x, m) & (x> x_ {0}) \ g (x, m) & (x leq x_ {0} ) end {matrix} right )
Phương pháp giải quyết
Bước 1: Tìm tập xác định của hàm số đã cho.
Bước 2: Khi (x neq x_ {0} ), xác định tính liên tục của hàm (f (x) ) trong các khoảng thời gian.
Bước 3: Khi (x = x_ {0} )
- Tính (f (x_ {0}) )
- Tính ( lim_ {x rightarrow x_ {0 ^ {+}}} f (x), lim_ {x rightarrow x_ {0 ^ {-}}} f (x) )
- So sánh ( lim_ {x rightarrow x_ {0 ^ {+}}} f (x), lim_ {x rightarrow x_ {0 ^ {-}}} f (x), f (x_ {0}) ) và rút ra kết luận tại điểm (x_ {0} )
Bước 4: Kết luận về tính liên tục trên tập xác định.
Dạng 3: Chứng minh rằng phương trình có nghiệm
Ví dụ: Chứng minh rằng phương trình (3x ^ {3} + 2x-2 = 0 ) có nghiệm trong khoảng ((0; 1) )
Hướng dẫn giải pháp:
- Xét hàm (f (x) = 3x ^ {3} + 2x-2 ) là một hàm đa thức liên tục trên R, tức là liên tục trong khoảng ((0; 1) )
- Ta có: (f (0) .f (1) = (- 2) .3 = -6 <0 )
- Xuất phát: (c epsilon (0; 1) ),
phương trình có nghiệm (c epsilon (0; 1) )
Trên đây là tổng hợp kiến thức về lý thuyết, cách giải cũng như một số bài tập điển hình. Hi vọng, bài viết đã cung cấp cho bạn những kiến thức bổ ích cho quá trình học tập của bản thân. Nếu có bất kỳ câu hỏi nào liên quan đến chủ đề chức năng liên tụchãy để lại comment, Tip.edu.vn sẽ hỗ trợ giải đáp cho bạn.
Xem thêm nhiều bài viết hay về Hỏi Đáp Toán Học
